The Remarkable Theory of Quantum Fields

There are lots of explanations and overviews of Quantum Mechanics (QM) out there on the web, but there aren’t very many devoted to Quantum Field Theory (QFT). The subject is notoriously inaccessible to those without a reasonably mature grasp of mathematics. Yet QFT is at the core of the Standard Model (SM) of particle physics – one of the greatest intellectual achievements of humanity.

Despite being tested experimentally for around fifty years, the SM’s predictions continue to check out, often to astonishing levels of accuracy.

I’m going to try and explain a little about QFT. Obviously this will be a gross over-simplification. But I hope I can convey at least a sample of this remarkable theory and the astonishingly simply assumptions that underly it.

In essence, QFT depends on three main sets of assumptions.

1. Causality. Any physical theory must preserve the order of events, regardless of the frame of reference of the observer. What this boils down to in practice is that the theory must be consistent with relativity.
2. Probability. This is basically the rules of QM.
3. Geometry. This goes by the fancy names of “gauge theory” and “group theory”. Essentially, rotations in different numbers of planes, not all of them in spacetime.

QFT takes these three, very basic, sets of assumptions, and then proceeds to ask the question, within these constraints, what is possible? The answer, almost magically, is largely the universe that we observe.

Over the next few weeks I hope to show how the theory works without going into great detail. Hopefully somebody will find some of this interesting.

p.s. There won’t be (much) maths.

The main thing you need to be comfortable with is the idea of a Probability Distribution (PD). The idea is very simple. As an example, suppose we ask every man in the country their height. Then we plot the number at each height.

We get a graph that looks roughly like this. This is supposed to be the usual “bell” graph. Lots of men are near the height in the middle and only a few are either very tall or very short.

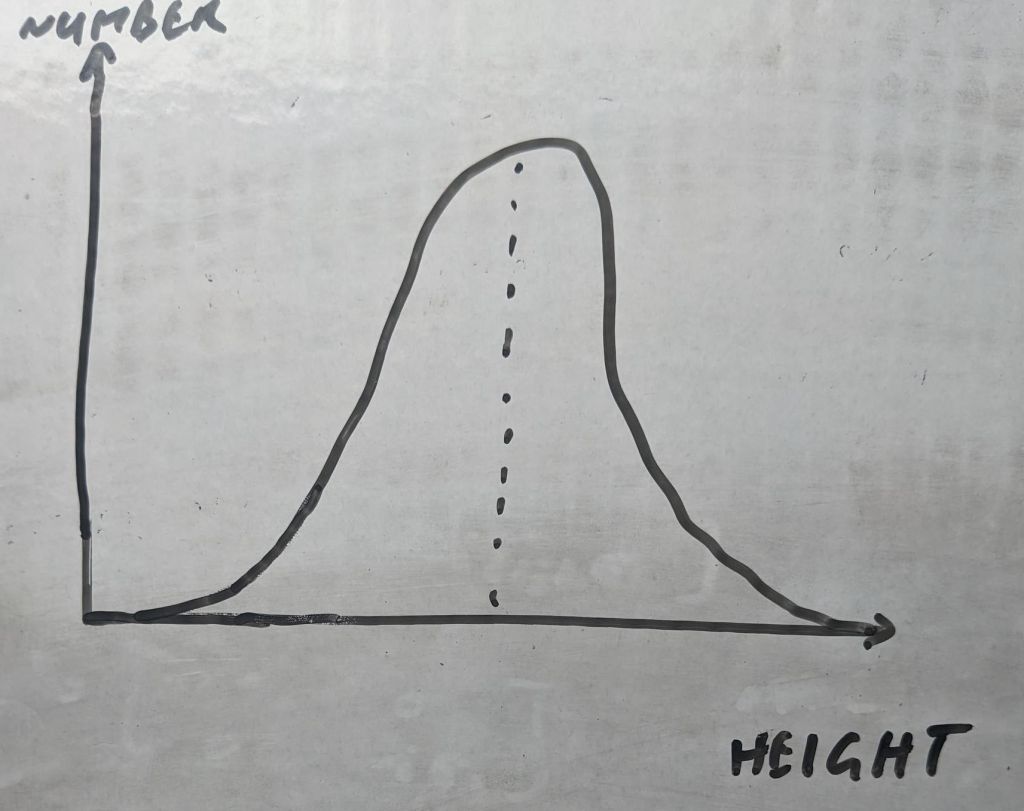
We can now simply relable the vertical axis as “Probability” instead of “number”. This is our PD.

We can ask what the probability is that a man is in a certain range of heights. The bigger the area under the curve between the heights marked A and B, the higher the probability that a man will be that height. For example, there is a much greater probability that a man is between the heights C and D than there is that he is between A and B.

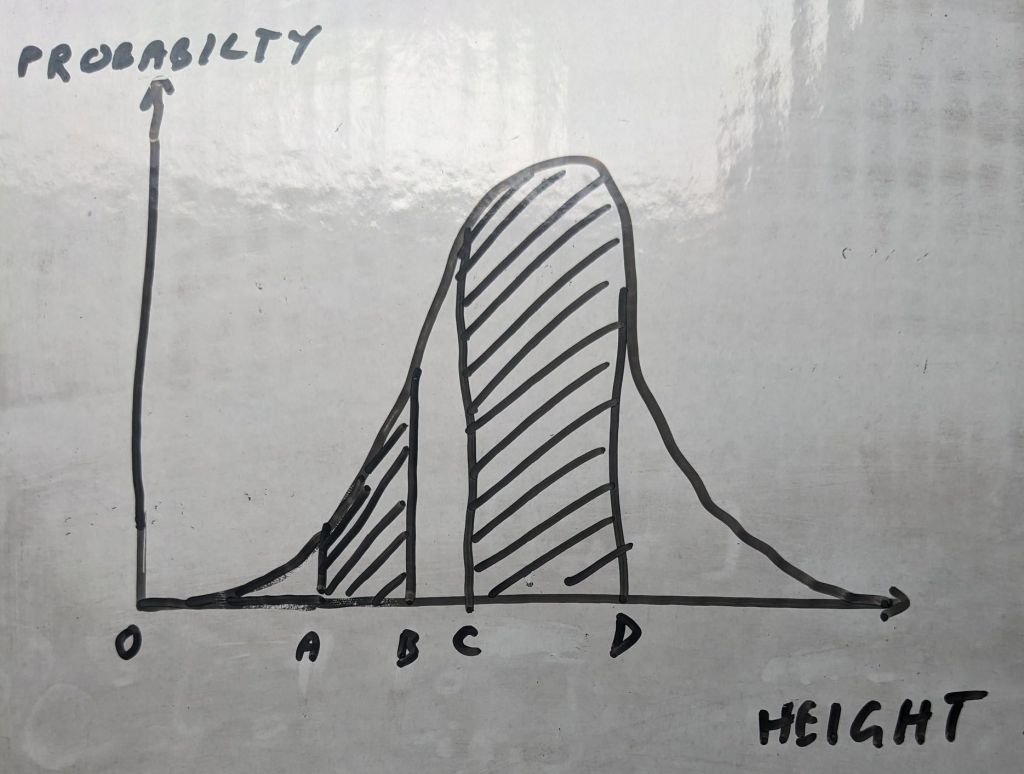
By convention, the total area under the curve is “1”. A probability of 1 is certainty. A man’s height is definitely between zero and infinity.

That’s all we need to know about probability for now. Next week, I’ll use this to build a summary of Quantum Mechanics, which we’ll need before moving on to QFT.